...
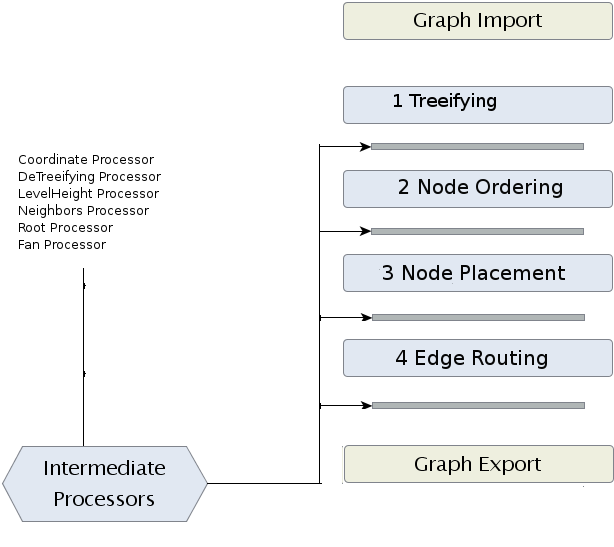
Mr. Tree is structured the same as its big brother KLay Layered. It consists of layout phases, intermediate processors, and a connected components processor. The picture below describes the control flow and therefore what is done when the tree algorithm operates.
This structure allow allows it to create independently independent phases for different aspects of the algorithm and to connect the phases through lightweight processorprocessors. In addtion addition this structure allows it to optimize and replace parts of the algorithm independently, and so to simplify the future development of the algorithm.
The architecture aims to separate the most main steps for layouting a tree . And and to be solve the layout taks by the divide and conquer principle. The individual steps are structured as following.
The first thing that is done is the graph import. Since the algorithm works with KIML, it is necessary to import the graph that should be layouted with Mr. Tree. The important data structure (KGraph) is a comparatively complex structure. The tree algorithm does not need all parts of this data structure, so the parts that are necessary are converted into a less complex data structure, the MrTGraph data structure (TGraph), which is described through a class diagram belowat its corresponding page. As mentioned before, Mr. Tree runs on that data structure. After execution of the tree algorithm, the TGraph gets reconverted to a KGraph in a graph export phase, so that everything works fine with KIML.
...
The first phase is named which the comparatively unfamiliar term "treeingtreeifying". "TreeingTreeifying" is a word that describes a process that builds a tree out of a graph that is no tree. In other words: Mr. Tree should also operate on graphs that are no trees, but that can be converted into trees. Imagine a graph that is nearly a tree. It contains one cycle that destroys the tree property. Now the first phase should detect that cycle, destroy it by removing the edge that destroys the tree property and reinsert that edge again after the tree algorithm was able to operate on that newly build tree.
Phase two and three calculate a place for every node in the layout. In phase two the nodes are ordered. They Their ordering depends on the weighting of each nodes. That means that nodes with many offspring and many following levels should be placed before nodes that do not have that many offspring or following levels. Phase two computes such a node ordering. Phase three then placed places the nodes. For placing the nodes, we use the algorithm developed by Walker et al. They developed a node positioning algorithm for general trees, that calculates x-coordinates for each node. This coordinates depend on many factors, such as position in a tree, number of offspring/ancestors and so on. A more detailed look can be found in the paper of Walker et al. which we also referenced in the Literature Section of this page.
...