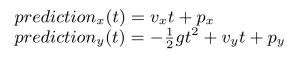The ball physics model's main objective is to provide a point in time to the controller, when the ball is predicted to be hittable, in order to not let the ball fall into the drain.
The code for what is described in this section can be found in the files "physics.cpp" and "physics.h".
Ball trajectory
The trajectory of a ball can be modeled to be parabolic. From two point p and p_old with corresponding timestamps, the velocity v is computed.
For a future point in time t, with t=0 being the timestamp of p, we can then approximately predict the corresponding ball position using the following formulas.
The incline of the playfield causes a vertical acceleration, which is modeled via a gravitational pull with the factor g = sin(6°) * 9.81 m/s².
The value of 6° is the incline of the playfield measured on the physical device.
Prediction
The controller calls the function full_prediction passing it two subsequent ball positions with timestamps. From these a ball trajectory is inferred as described above.
Along the trajectory future times are stepwise tested for whether the corresponding predicted position is in the flipper range.
Once a position inside the flipper range is found the search is continued both forwards and backwards in smaller steps in order to find a good enough estimate of the first and last possible time to hit the ball.
If the trajectory does not intersect the flipper range within a certain prediction frame (see below "Prediction parameters") a value far enough into the future is returned, that will be overwritten by subsequent predictions.
With the current configuration the controller uses the middle point in time between the first and last possible time in order to be most positive to hit the ball.
The computed velocity is also passed to the controller and used is some more advanced tactical decisions like catching balls.
Configuration
Prediction parameters
| Parameter | Description | Default value |
|---|---|---|
| PREDICTION_FRAME | window size for prediction - How far into the future are predictions calculated at most. | 70ms |
| PREDICTION_STEP_SIZE | size of the steps for the forward search | 10ms |
| REFINEMENT_FACTOR | The prediction step size for the reverse search is | 10 |
When setting the PREDICTION_FRAME keep in mind that predictions, that reach multiple frames into the future, are likely to be overwritten, when new frames arrive and new predictions are calculated.
Nevertheless it is reasonable to calculate predictions beyond the next frame in case a ball is not recognized on the next frame.
With the default values up to 7 predictions are calculated if the ball is not predicted to be in flipper range roughly within the next two frames.
The REFINEMENT_FACTOR is also the worst case number of predictions calculated during the reverse search part of the prediction process.
Flipper range
The model of the area, where the the flippers can hit a ball is computed from a set of five points. These points are set to real world coordinates in meters
and should not need further adjustment after the camera is correctly calibrated (see World Coordinate System).
The values for the left flipper are set to be symmetrical.
| Point# | Description |
|---|---|
| 1 | center point of the circle that the flippers tip moves o |
| 2 | highest point a ball can be at when it hits the resting flipper |
| 3 | lowest point a ball can be at when it hits the resting flipper |
| 4 | lowest point a ball can be at when it hits the fully triggered flipper |
| 5 | highest point a ball can be at when it hits the fully triggered flipper |
From these points an area, where the ball is deemed to be hittable, is computed.
Inlane Area
Since the trajectory prediction does not consider collisions in general, we need a different kind of predictions for the inlanes,
i.e. the path feeding a falling ball from the playfield to the flippers, behind the slingshot.
A ball is considered to be in an inlane, when it is in a rectangular area, with one edge given by the beginning of the flipper
and the other by a point at highest, outermost position of the angled part of the inlane.
In this area the vertical acceleration is deactivated in the prediction, since it would cause the prediction to assume the ball would slide into the wall.
Though in reality there is still some acceleration, a simple linear prediction has shown to be practical in this less critical area.